PiMA

Posted on: 15/1/2019

---

Bạn chắc hẳn đã quen thuộc với những hình đa giác đều trong mặt phẳng 2 chiều như tam giác đều, hình vuông, ngũ giác đều, lục giác đều,… Và có thể đôi khi bạn sẽ thắc mắc, nếu trong trường hợp không gian 3 chiều thì sẽ như thế nào? Liệu có tồn tại các khối đa diện đều chứ, và nếu có thì chúng sẽ trông như thế nào?

Câu trả lời là có, và trên thực tế là có khá nhiều loại khối đa diện đặc biệt trong hình học. Trong bài viết này, chúng ta sẽ nói về các khối đa diện đều lồi - hay còn được gọi là các khối đa diện Plato.

Ngày xưa, các nhà triết học cổ đại cho rằng vật chất được tạo thành từ 4 nguyên tố cơ bản là đất, nước, lửa, khí. Nhà triết học người Hy Lạp Plato (khoảng 427 – 347 TCN) cho rằng các nguyên tố này tương ứng với các khối đa diện lồi đều trong hình học. Khối tứ diện đều (tetrahedron) ứng với lửa. Khối lập phương (hexahedron hoặc đơn giản là “cube”) ứng với đất. Khối bát diện đều (octahedron) ứng với khí. Khối 20 mặt đều (icosahedron) ứng với nước. Khối cuối cùng là khối 12 mặt đều (dodecahedron) mà ông cho rằng Chúa dùng để sắp xếp các chòm sao trên bầu trời.

Sau này, Aristotle mới thêm vào một nguyên tố thứ 5 là “ether”, nguyên tố tạo nên khoảng không gian của vũ trụ, nhưng ông không có ý định gắn nguyên tố thứ năm này với khối 12 mặt của Platon.

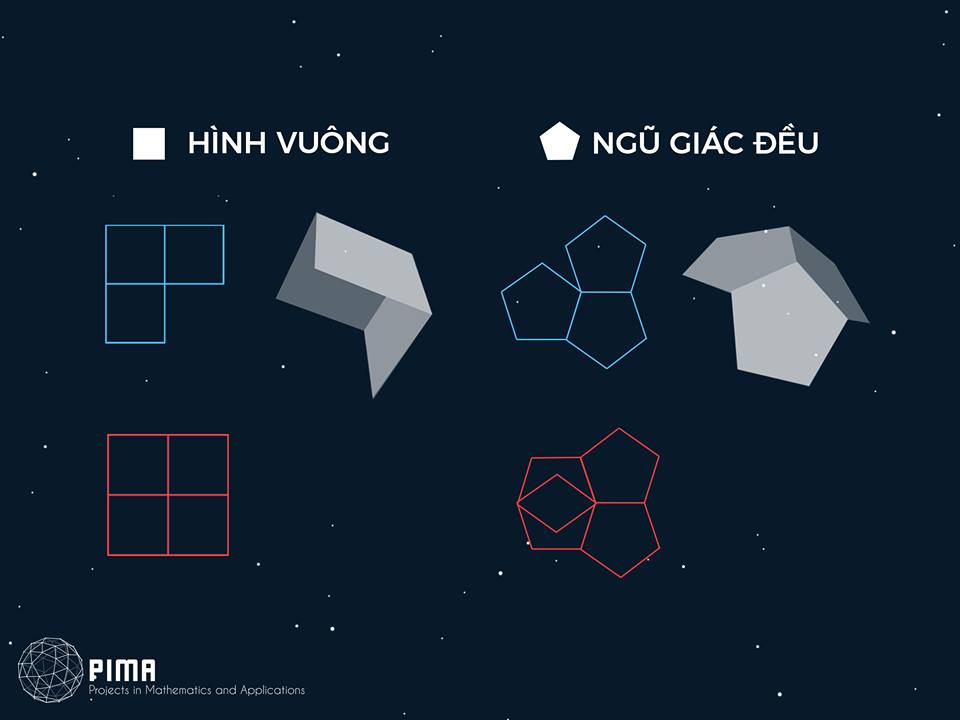
Hãy quan sát kĩ hơn hình dạng của các khối Plato – các khối đa diện lồi đều này. Ta dễ thấy rằng các mặt và các cạnh của mỗi khối đều bằng nhau. Khối tứ diện đều có các mặt là 4 tam giác đều bằng nhau, và mỗi đỉnh của khối là đỉnh chung của 3 mặt. Khối bát diện cũng được tạo thành từ các tam giác đều, nhưng mỗi đỉnh là đỉnh chung của 4 mặt. Tương tự, khối 20 mặt đều có mỗi đỉnh là đỉnh chung của 5 mặt tam giác đều. Nếu ta thử tạo một khối đa diện đều bằng hình vuông, ta được một khối duy nhất là khối lập phương quen thuộc. Tương tự, ta có duy nhất một khối tạo từ hình ngũ giác là khối 12 mặt đều.

Trong toán học, ta thường dùng kí hiệu Schläfli dưới dạng {p, q} để kí hiệu các khối này, trong đó p là số cạnh của mỗi mặt, q là số mặt tạo nên một đỉnh của khối. Như vậy, kí hiệu của khối tứ diện đều sẽ là {3, 3} và khối lập phương sẽ là {4, 3}, v.v.

Bạn có nhận ra là chỉ có duy nhất 5 khối đa diện lồi đều không? Trong khi đó đối với các đa giác đều trên mặt phẳng hai chiều, chúng ta có thể tạo ra một đa giác đều với bao nhiêu cạnh cũng được, từ tam giác đều, tới hình vuông, hình 7 cạnh đều, hình 8 cạnh đều,… có thể lên tới hàng chục, trăm cạnh tùy ý. Vậy tại sao chúng ta lại không thể có điều tương tự trong không gian 3 chiều?

Trên thực tế ta có thể kiểm chứng điều này một cách đơn giản, cần một vài tờ giấy, kéo và một chút băng keo thôi.

Đầu tiên chúng ta thử tạo một khối từ các hình tam giác đều.

Bắt đầu với 3 hình tam giác đều cùng một đỉnh, dán 2 cạnh với nhau, ta đã được một khối tứ diện khuyết một mặt. Tiếp theo ta thử 4 tam giác chung một đỉnh thì được một nửa của hình bát diện rồi. Tiếp theo lại thử với 5 tam giác đều, ta được một phần của khối 20 mặt đều. Với 6 tam giác chung một đỉnh, 6 góc của 6 tam giác này cộng lại với nhau vừa đúng 360 độ, chúng cùng nằm trong một mặt phẳng nên ta không thể tạo một khối có 6 tam giác đều chung một đỉnh được. Vậy ta chỉ có thể tạo 3 loại khối có các mặt là các tam giác đều thôi.

Tương tự, lại tiếp tục thử với các hình vuông.

Khi dán 3 hình vuông lại với nhau, bạn dễ thấy ở đây là một nửa của khối lập phương quen thuộc. Khi có 4 hình vuông, 4 góc 90 độ lại cùng nằm trong một mặt phẳng nên ta cũng chỉ tạo được một khối từ hình vuông.

Cuối cùng là hình ngũ giác.

Dán 2 cạnh của 3 ngũ giác đều chung một đỉnh ta được một phần của khối 12 mặt này. Khi ta thử với 4 hình ngũ giác, tổng các góc của chúng lớn hơn 360 độ nên ta cũng không tạo được thêm hình khối nào.

Khi thử đến hình lục giác, 3 khối lục giác chung một đỉnh, một lần nữa, lại lát kín một mặt phẳng, nên ta cũng không tạo được khối nào từ các lục giác đều. Các khối 7 cạnh, 8 cạnh… v.v cũng vậy, vì tổng các góc của chúng quá lớn. Đây là lý do ta chỉ có đúng 5 loại khối đa diện lồi đều trong không gian 3 chiều.