Khám phá Reinforcement Learning (Kỳ 2)

Posted on: 25/6/2019

Như đã giới thiệu ở Kỳ I, mô hình reinforcement learning mô tả quá trình người học tương tác với môi trường (theo mốc thời gian t) thông qua việc lựa chọn hành động từ tập A. Các hành động thay đổi trạng thái từ tập S của môi trường và nhận được các giá trị đánh giá từ tập R. Trong thực tiễn áp dụng, A thường được biết trước còn việc xây dựng cơ sở dữ liệu cho S và R dựa vào việc thử nghiệm và đánh giá trong quá trình huấn luyện (training).

Để gần với thực tế, ta cho phép các hành động thay đổi trạng thái của môi trường một cách ngẫu nhiên, ứng với một xác suất nhất định. Với mỗi hành động, xác suất này độc lập với trạng thái trong quá khứ khi biết được trạng thái hiện tại (để dễ hình dung, bạn có thể nghĩ đến trạng thái bàn cờ khi đánh theo một chiến thuật ngẫu nhiên nào đó). Trong Toán học, tính chất trên được gọi là tính chất Markov và quá trình tương ứng được gọi là một Markov process.

Quá trình ngẫu nhiên Markov (Markov process)

Để đơn giản, ta giả sử có hữu hạn các trạng thái $S = {s_1, s_2, \dots, s_n}$ và gọi trạng thái ở mốc thời gian $t$ là $S_t$ (bạn đọc biết về xác suất cơ bản sẽ nhận ra $S_t$ tương ứng với một biến ngẫu nhiên). Markov process là một quá trình thay đổi trạng thái ngẫu nhiên, ứng với dãy giá trị của biến ngẫu nhiên $S_0, S_1, S_2, \dots$ thỏa mãn tính chất Markov. Trong ngôn ngữ Toán học, tính chất Markov có thể được viết lại dưới dạng xác suất có điều kiện (conditional probability):

\[Pr(S_{t+1} | S_t , S_{t-1}, …, S_0) = Pr(S_{t+1} | S_t)\]

Ví dụ 3: Giả sử ngày mai có mưa hay không chỉ phụ thuộc vào thời tiết hôm nay. Bé Trabbit (mới 5 tuổi) nhận ra nếu hôm nay không mưa thì khả năng 80% ngày mai cũng không mưa, còn nếu hôm nay mưa thì khả năng 40% ngày mai cũng sẽ mưa.

  •  $S =$ {không mưa, mưa}, $Pr (S_{t+1} = $ không mưa $\vert S_t =$ không mưa) = 80%;
  •  $Pr (S_{t+1} =$ mưa $\vert S_t =$ không mưa) = 20%, $Pr (S_{t+1}$ = mưa $\vert S_t =$ mưa) = 40%;
  •  $Pr (S_{t+1} =$ không mưa $\vert S_t =$ mưa) = 60%.

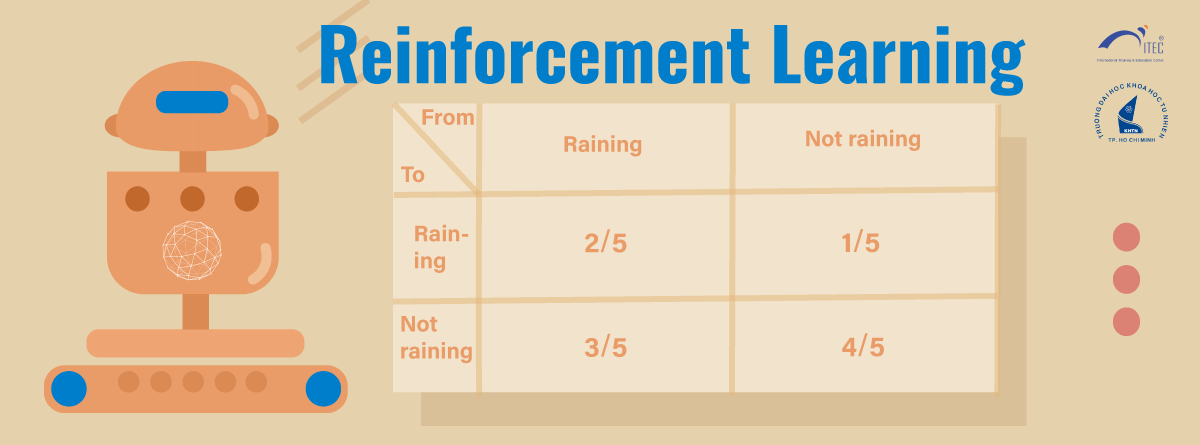
Ta có bảng xác suất chuyển trạng thái (transition probability) sau:

Đến đây, bạn đọc biết về đại số tuyến tính cơ bản (linear algebra) sẽ nhận ra bảng trên chẳng qua chỉ là một ma trận (matrix). Thật vậy, một Markov process gồm n trạng thái hoàn toàn tương đương với một ma trận vuông gồm n dòng và n cột thỏa mãn một số tính chất nhất định. Ma trận và đại số tuyến tính cho phép việc tính toán và nghiên cứu các Markov process với kích thước lớn trở nên dễ dàng hơn rất nhiều.

Trở lại với ví dụ 3, ta có thể thấy xác suất chuyển trạng thái không phụ thuộc vào thời điểm t. Một Markov process thỏa mãn tính chất này được gọi là ổn định (stationary transition). Bé Trabbit nhận thấy hôm nay trời mưa ($S_0$ = mưa), và nhờ biết một ít xác suất cơ bản, bé tính được giá trị kì vọng của số ngày mưa:

  • sau 2 ngày (tính cả ngày 0) là 7/5;
  • sau 3 ngày là 42/25;
  • sau 10 ngày là khoảng 3.7 ngày;
  • sau 30 là khoảng 7.8 ngày;
  • sau 60 ngày là khoảng 15 ngày; …

Đến đây, bé chợt nhận ra tỉ lệ ngày có mưa trên tổng số ngày càng ngày càng gần 1/4 (bạn đọc biết về giải tích cơ bản sẽ nhận ra đây là giới hạn của dãy số trên).

Rất đáng kinh ngạc, nhà Toán học người Nga Andrei Markov đã chứng minh được phỏng đoán trên: Một Markov process ổn định có hữu hạn trạng thái luôn đạt đến một phân bố xác suất bão hòa (equilibrium distribution) bất kể trạng thái ban đầu. Markov process cùng với kết quả lý thuyết kỳ diệu này là cơ sở của thuật toán PageRank làm nên tên tuổi của Google.

Trở lại với reinforcement learning, qua bài viết kỳ này, ta đã hiểu được về quá trình ngẫu nhiên tương ứng với một hành động nhất định (chẳng hạn trong Ví dụ 3, hành động duy nhất là chờ qua ngày). Trong kì tiếp theo, chúng ta sẽ xem xét tất cả các hành động trong A cùng lúc và xây dựng mô hình lựa chọn giữa chúng một cách tối ưu nhất (Markov Decision Process).

Bài tập cho bạn đọc: Trong Ví dụ 3, các số 20% và 60% có từ đâu? Điều kiện của một ma trận vuông tương ứng với một Markov process là gì? Kiểm tra tính toán của bé Trabbit (gợi ý: tính xác suất ngày thứ t có mưa theo t trước)

TÀI LIỆU THAM KHẢO:

TRẠI HÈ TOÁN HỌC VÀ ỨNG DỤNG 2019
Thông tin chi tiết: http://bit.ly/PiMA2019_Info
Đơn ứng tuyển: http://bit.ly/PiMA2019_Application
Hạn chót nộp đơn: 23h59’ ngày 20/6/2019

Mọi thắc mắc xin vui lòng liên hệ:

  • Email: pima.vn@gmail.com
  • Fanpage: fb.com/pimavn
  • Hotline: 0961565087 (Thế Anh)